背景

不平衡数据集是机器学习特别是分类器模型训练过程中普遍存在的挑战，尤其是在异常检测领域，比如医疗检测、欺诈信息检测等，我们更加关注的是异常类，然而异常数据的发生概率较小，最终导致训练数据中的类别不平衡。当一个类别中的样本数量明显超过另一类时，模型往往会偏向大多数样本，从而导致性能不佳。

针对数据不平衡问题，可以通过调整损失函数，使模型在少数类出错时承担更高的代价，从而引导模型更多关注少数类。同时，也可以直接从数据源头进行干预，修改数据集以缓解不平衡。具体来说，常用的两种方法是：

  1. 欠采样：通过随机删除或基于某种规则减少多数类样本数量，缺点是删除样本可能会损失有意义的信息
  2. 过采样：通过复制样本或利用样本生成技术增加少数类样本数量，缺点是引入噪声，通过复制而来的样本可能使得模型对某些类别过于敏感

这里我们主要介绍传统的过采样技术——SMOTE，及其改进算法。

性能指标

在一般情况下，许多分类算法的目标是最大限度的提高分类准确率，而分类准确率是一个偏向多数类的指标。在上文我们提到，异常样本的占比机极小，假定只有0.1%是不合法的，那么什么都不做将所有样本都认为是合法的正确率也有99.9%，但这无疑是没有任何意义的。所以我们需要更适合针对数据不平衡问题的评价指标，混淆矩阵是最基本、最直观、计算最简单的方法。

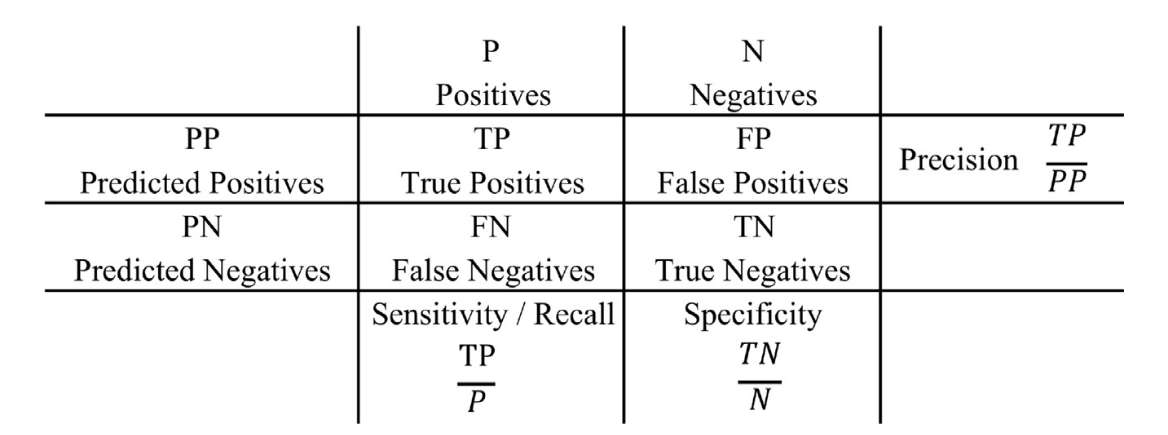
1746447887525.png

  • 精准率：所有被预测为阳性的样本中真实阳性的占比，强调预测结果的可靠性。
  • 召回率/敏感度：所有阳性样本被正确预测为阳性的概率，强调不能漏掉真正的。
  • 特异性：所有阴性样本被正确预测为阴性的概率，强调不误伤好人。

精准率与召回率看上去类似，但实际意义截然不同。当精准率高时，表明预测结果很精准，但可能很多阳性没有被发现；当召回率高时，表明发现了越多的阳性，但可能将部分阴性预测为阳性，导致精准率不那么高。所以，这两者是很难求得两全的标准，为了综合精准率和召回率二者的表现，出现了F1分数，计算公式如下。

从公式可以看出，F1 指标对精准率和召回率的权重是相等的，二者并未偏向任何一方。如果需要对精准率和召回率的重要性进行权衡，还可以使用加权的 ——F1 的广义形式，时即为F1，则更重视召回率，反之则更重视精准率。

上文中提到的精准率、召回率等等指标都是只关注阳性的识别质量，在一些场景如信用卡欺诈检测，我们也不能只关注正类，要同时保证正类和负类都很好才能得到高分，这是G-mean就派上用场。

SMOTE

介绍

论文地址

英文全称 Synthetic Minority Over-Sampling Technique，即合成少数类过采样技术，是一种十分经典的过采样技术。正如其名，旨在通过在特征空间生成新的少数类样本来弥合差距。简易流程如下图所示。

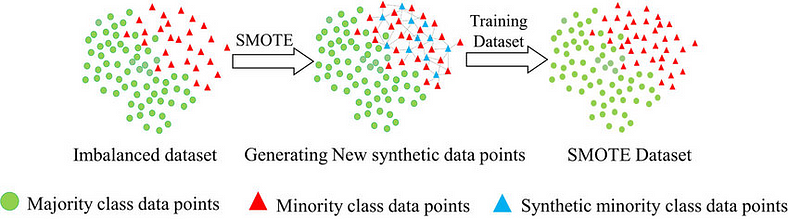
6810e83b1ab50.png

具体实现

  1. 首先统计各类别的样本数量，识别出少数类样本

  2. 选定一个少数类样本点，找到它在特征空间内距离最近的K个少数类邻居

  3. 随机选择一个邻居，在原样本和邻居之间连线，并在该线上进行随机位置插值，生成新的少数类样本 $$ 其中为选定的样本，为随机选择的邻居，

缺点
  • 虽然通过线性插值的方式避免了直接复制带来的过拟合风险，但是如果少数类分布本身比较分散，线性插值可能生成不合理样本即引入噪声。
  • 无法解决类别重叠问题，少数类与多数类在特征空间重叠严重，SMOTE可能会进一步加剧混淆。
  • 对所有少数类样本一视同仁，并未考虑近邻样本的类别信息，往往出现样本混叠现象。
  • 在存在噪声的情况下，可能会在多数区域生成少数样本，加剧了类内部平衡现象，如下图所示。

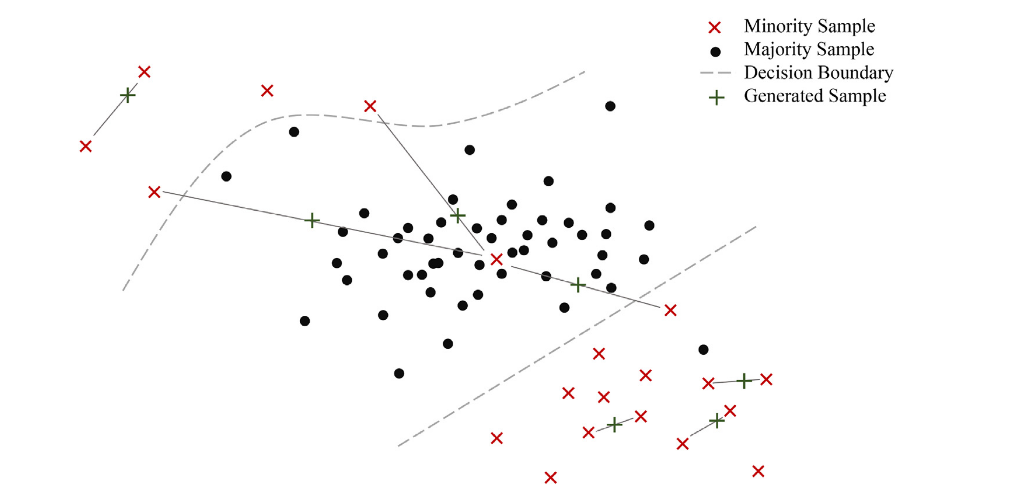
Borderline-SMOTE

介绍

论文地址

是在SMOTE基础上改进的算法，仅使用边界上的少数类样本合成新样本，从而改善样本的类别分布。更具体地，Borderline-SMOTE作出的改进如下：

传统smote对所有少数类样本进行过采样；而bl-smoe会先根据邻近样本的类别信息对少数类样本进行如下分类，其中重点关注危险区域

  • Safe安全区域：最近邻中多数类的数量少于一半，认为少数类聚集且远离多少类，不必生成样本徒增计算量
  • Danger危险区域：最近邻中多少类数量超过一半但不全是，认为样本靠近边界，容易被错误分类
  • Noise噪声区域：最近邻中全部是多数类样本，认为该样本为噪声样本
实现细节

Borderline-SMOTE1：从危险区域的每个样本的k个少数类最近邻中随机选择s个，生成合成样本，沿样本与其最近邻之间的线段插值。

Borderline-SMOTE2添加额外改进：利用最近的多数类邻居进行插值，但，即更靠近少数类，避免类间重叠。

采样前后对比

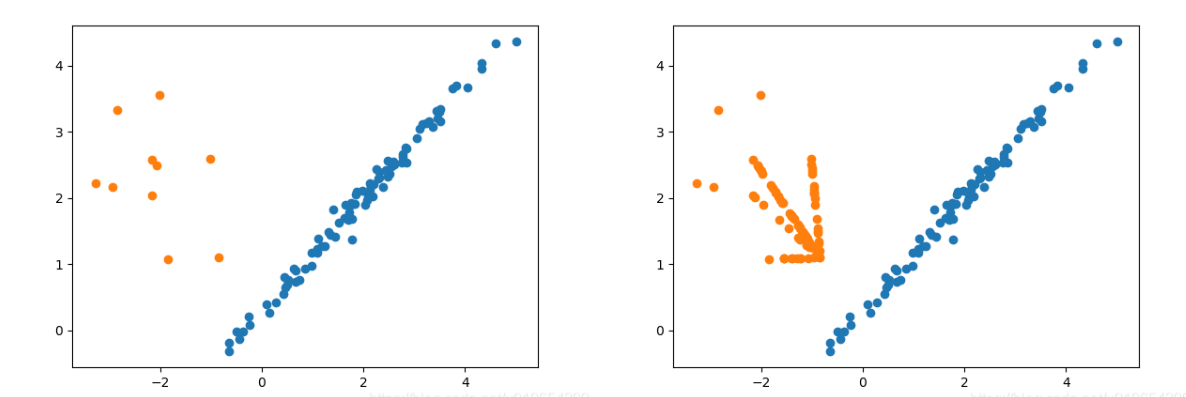
1745850505162.png

ADASYN

介绍

论文地址

全称 adaptive synthetic sampling，即自适应合成抽样，与Borderline-SMOTE相似，同样是基于”SMOTE在合成样本时对所有少数类一视同仁”这一问题加以改进。而ADASYN提出，要重点照顾分类困难的少数类样本，让模型自适应地更关注这些“难学”的地方。核心思想：

  • 对于周围多数类较多的少数类，类似bl-smote中的危险区域，被认为是难学，生成更多的合成样本
  • 而对于周围多数类较少的少数类，类似bl-smote中的安全区域，被认为是易学的，生成较少或不生成合成样本
算法流程
参数说明
  • 分别为多数类和少数类样本数
  • 最大容忍阈值
  • 最终数据集平衡程度
处理过程

  1. 计算不平衡度

  2. 检查是否需要生成合成样本， 说明数据集不平衡程度超出了容忍阈值，需要生成合成样本。

  3. 计算样本数量总数

  4. 计算学习难度 其中 是K近邻中多数类样本数。反映了样本的学习难度，即周围多数类越多，学习难度越大。

  5. 归一化学习难度，此时可以看作是概率分布，表示每个少数类样本的相对权重

  6. 根据学习难度分配合成样本数

  1. 生成合成样本，在K近邻中随机选择一个少数类样本

采样前后对比

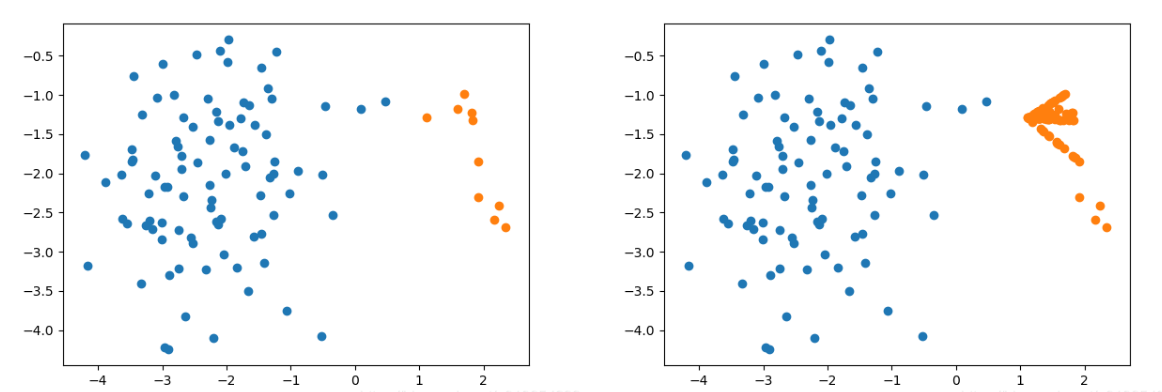
评价

从算法流程上可以看出，同样是关注少数类样本周围的样本数量，ADAYSN的适应性更强，并不是硬性区分周围多数类样本超过半数的区域为危险区域，而是利用学习难度这一标准加以权衡，让少数类样本之间有着更高的区分度，而不只是简单的危险和安全。

算法比较

论文地址

该论文对SMOTE和ADASYN算法进行比较分析，主要探究预处理方法、分类器的选择和数据的不平衡程度对模型性能的影响程度。

过采样设定为使少数类和多数类的样本数尽可能相等，分类模型选择逻辑回归、随机森林、支持向量机。

实验结果分析

总体上来看，SMOTE和ADAYSN在绝大多数情况都能显著提高分类器性能，表明过采样有效改善了少数类的预测能力。但是并没有一种预处理方法在所有场景下始终优于另一种

模型的影响
  • SVM 随着不平衡程度的增加，SMOTE+SVM的组合表现更佳且均优于ADAYSN
  • RF ADAYSN表现较优，随着不平衡程度增加，性能提升更明显
  • LR 在不平衡程度最高的信用卡欺诈数据中，过采样反而降低了性能，可能是由于合成样本引入了噪声
讨论

过采样率统一设为完全平衡（50:50），可能不适用于所有数据集，论文建议在某些场景下尝试较低的过采样率或使用其他方法以减少合成样本的负面影响。

实际上，更加值得考虑的问题是，Borderline-SMOTE和ADAYSN都只是针对“传统SMOTE合成样本时对所有少数类一视同仁“这一问题进行改进，并没有解决生成不合理样本和类别重叠问题，单纯的过采样反而加重边界模糊，特别是在少数类样本分散或存在离群点时。

K-means SMOTE

研究背景

论文地址

引言部分指出，在类不平衡的情况下，改进分类技术可以分为三大类：算法级方法、数据级方法、成本敏感方法。算法级方法受限于分类器，相比之下，对成本敏感的方法旨在为每个类别提供不同误分类成本的分类算法。这就需要了解误分类成本，而误分类成本取决于数据集，通常是未知的或难以量化的。所以，数据级方法因其通用性得以普遍适用。

数据集方法可以进一步划分为随机方法和知情方法。随机方法是随机选择要删除和复制的样本，而知情方法则不同。它考虑到了样本的分布情况。这样，有信息的方法就能将精力集中在输入空间的关键区域，例如Borderline-SMOTE中的安全区域。因此，有信息的方法可以避免产生噪音，并能解决类内的不平衡问题。

介绍

结合K-means聚类和SMOTE的过采样方法，旨在消除类间不平衡和类内不平衡问题。

k-means是一种非常常用的无监督聚类算法，目标将数据划分为K个簇，使得每个簇内的数据点尽可能相似，而不同簇之间的数据点尽可能不同。它的核心思想是最小化簇内样本的平方误差。

算法流程:

  1. 初始化：随机初始化聚类中心。
  2. 分配样本：每个样本分配到最近的聚类中心，形成K个簇。
  3. 更新中心：重新计算各簇所有点的均值，作为新的聚类中心。
  4. 重度23操作，直到聚类中心不再变化或达到最大迭代次数。
算法流程
聚类预处理

使用k-means聚类算法将整个数据集划分为k个簇，聚类的目的是识别数据的自然分组，为后续的过采样提供结构化的基础。该步骤的核心目标是识别生成合成样本区域。

过滤与采样分配

  1. 根据每个簇的不平衡比率选择适合采样的簇，不平衡程度的定义如下 默认情况下，选择少数类样本占比至少为50%的簇（），也可以通过来控制

  2. 计算每个簇的稀疏度，作为采样权重，稀疏的少数类簇获得更高的采样权重。下面分别是密度、稀疏度、采样权重,采样数量的计算公式

过采样

依然采用样本和邻居之间进行线性插值的方法，随机选择簇内少数类样本，在其k近邻中随机选择少数类样本，生成新样本，是随机权重

评价

观察算法流程，在过滤操作和Borderline-line比较类似，都是对不同少数类样本加以区分或者关注；在生成样本数量分配上，和ADAYSN算法过程比较类似，增加对稀疏区域的采样数量。该算法得以效果显著的原因在于 K-means预处理。

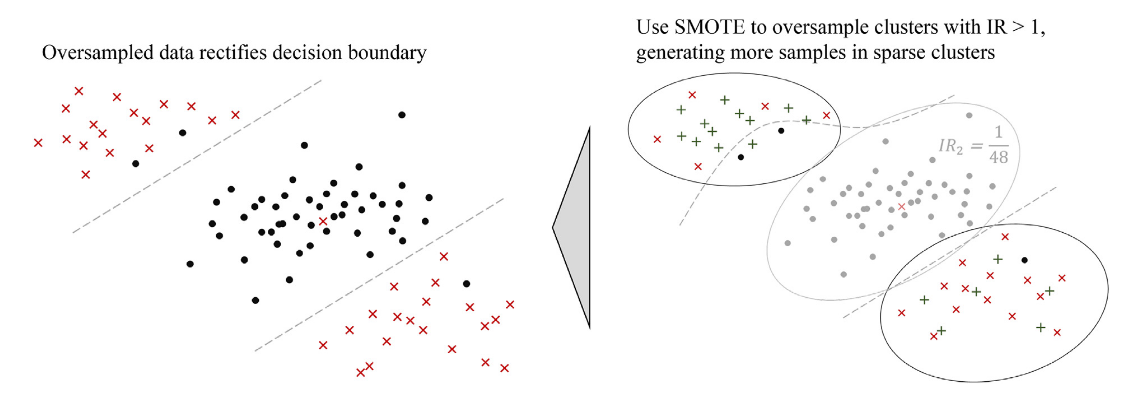
K-means是一种无监督的聚类方法，不依赖于类标签，直接对整个输入空间进行聚类。这允许算法发现类重叠区域，并通过过滤步骤排除这些区域，仅在少数类主导的簇内过采样。如下图所示，最终得到过采样数据校正决策边界。

6810e299cc890.png

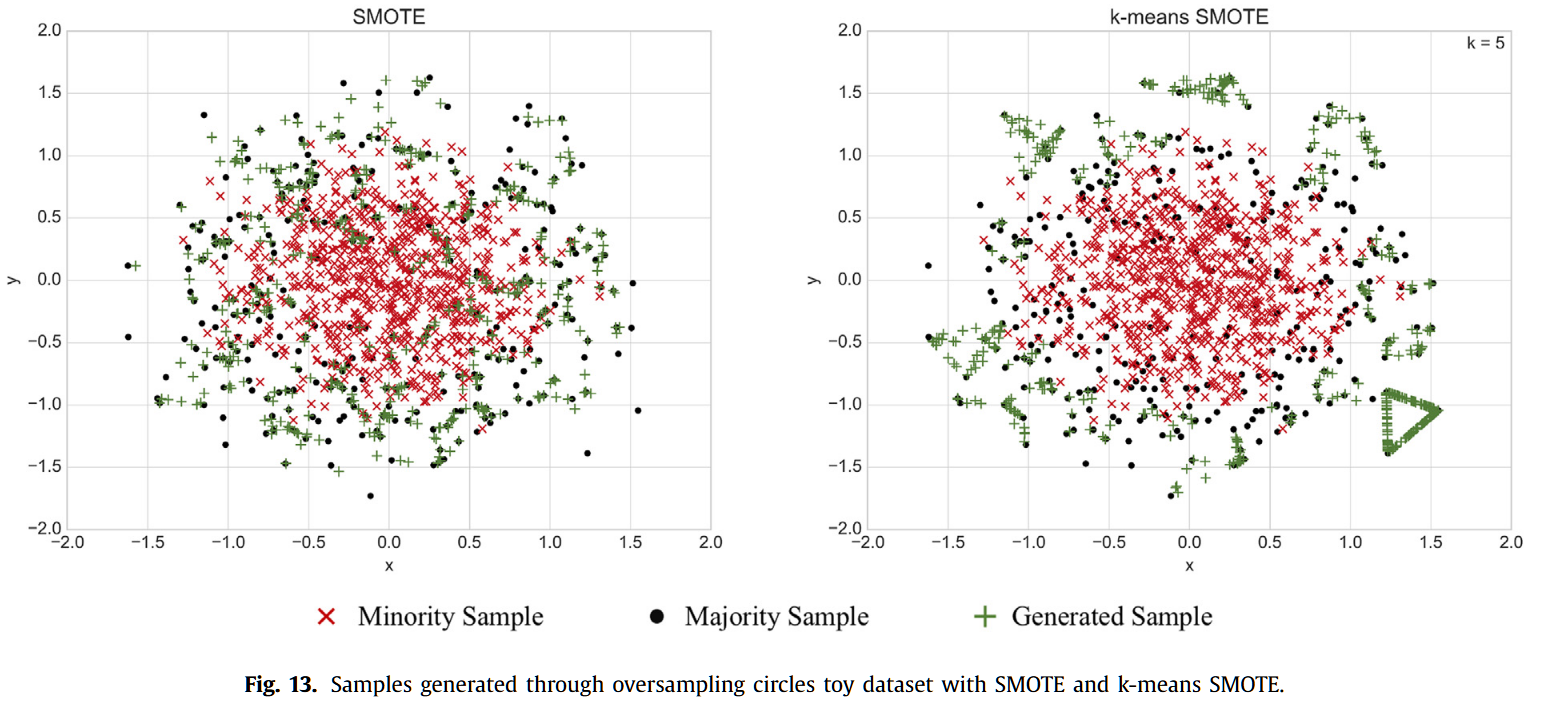
SMOTE和k-means SMOTE过采样之后的数据分布对比，可以明显看出k-means SMOTE避免在重叠区域生成样本，保护了决策边界的清晰性，改善分类器的泛化能力。

6810d65055836.png

与其它聚类算法的比较

  • CURE-SMOTE：使用层次聚类清除噪声，但其复杂度较高，未解决类内不平衡问题
  • SOMO：将数据映射到二维空间，增加了预处理的复杂性，还可能丢失掉高维信息
  • Cluster-SMOTE：仅聚类少数类样本，无法识别类重叠区域，K-means的全局聚类更加全面